Goal¶
- Understand the past, current, and future of RL.jl
- Master how to apply RL.jl to some interesting problems
- Learn how to define the problem we want to solve with RL.jl
About Me¶
- Master's degree on NLP at University of Chinese Academy of Sciences in 2016.
- Getting started to use Julia at
v0.6around 2017. - I'm also an active member in the JuliaCN community in China.
- My last job at Microsoft was mainly about NLU in dialog systems.
- Joined a startup (inspirai.com) focuing on NLP & RL in games last month.
(Not a serious RL researcher, correct me if I'm wrong)
(Non-native speaker, interrupt me if I don't make myself clear)

- It was named
TabularReinforcementLearning.jlat first - Johanni Brea sent me the invitation to work on it together
- Implemented several tabular RL related algorithms from the famous book Reinforcement Learning: An Introduction
- Many deep RL related algorithms are implemented following that.
- DQN related variants (relatively fast)
- Policy Gradient related variants (pretty fast)
- CFR related variants
- Offline RL
Far from perfect.
- Documentation is poor.
- Not easy to learn for newbies.
- No support for async/distributed RL.
- Limited support for multi-action space environments.
(Most of them will be addressed in the next release this summer!)
A Practical Introduction¶
The standard setting for reinforcement learning contains two parts:
- Agent
- Environment
env |> policy |> env

More specifically:

Let's see a more concrete example:
]activate .
]st
using ReinforcementLearning
using StableRNGs
using Flux
using Flux.Losses
using IntervalSets
using CUDA
using Plots
The Environment¶
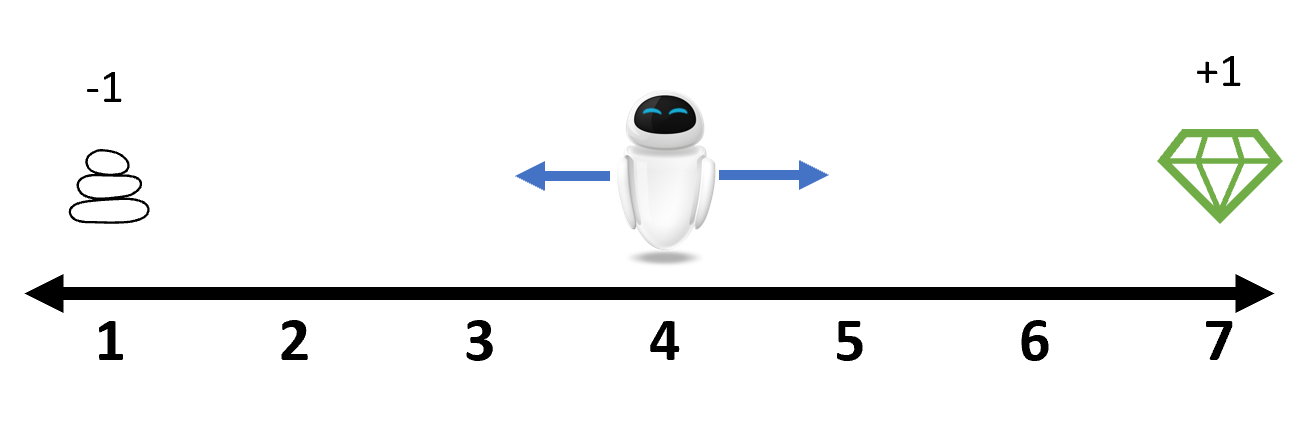
env = RandomWalk1D();
state(env)
reward(env) # though it is meaningless since we haven't applied any action yet
action_space(env)
env(2)
state(env)
The Policy¶
Actually, the policy could be arbitraray callable object which takes in an environment and returns an action.
policy = RandomPolicy(action_space(env))
[policy(env) for _ in 1:10]
Now we have both police and environments.
Q1: How to simulate the interactions between policies and environments?¶
run(policy, env)
It seems nothing happened???
state(env), reward(env), is_terminated(env)
@which run(policy, env) # run until the end of an episode
Q2: What if we want to stop after several episodes?¶
run(policy, env, StopAfterNEpisodes(10))
Q2.b: What if we want to stop until arbitrary condition meets?¶
Well, in that case, you need to implement your customized stop condition here. In RL.jl, several common ones are already provided, like:
StopAfterNStepsStopAfterNEpisodesStopAfterNSeconds- ...
How to implement the customized stop condition is out-of-scope today. In short, you only need to implement (condition::YourCondition)(agent, env) to return true when you want to stop the run function.
Q3: How to collect experiment results?¶
More specifically,
- How many steps in each episode?
- What's the total reward of each episode?
- How much has our policy improved in the whole experiment?
- ...
To answer these questions, many hooks are introduced in RL.jl.
run(policy, env, StopAfterNEpisodes(10), TotalRewardPerEpisode())
Any question until now?¶
A Closer Look into Policies and Environments¶

The Actor Mode¶
In most cases, when you execute run(policy, env, stop_condition, hook), the policy is running in the actor mode. Or someone would call it the test mode. Because here the policy won't try to optimize itself.
(As in the picture above, the data from the environment flows into the policy directly)
Let's see another example:
S, A = state_space(env), action_space(env)
NS, NA = length(S), length(A)
policy = QBasedPolicy(
learner = MonteCarloLearner(;
approximator=TabularQApproximator(
;n_state = NS,
n_action = NA,
opt = InvDecay(1.0)
)
),
explorer = EpsilonGreedyExplorer(0.1)
)
policy(env)
run(
policy,
RandomWalk1D(),
StopAfterNEpisodes(10),
TotalRewardPerEpisode()
)
Why?¶
[policy.learner(s) for s in state_space(env)] # the Q-value estimation for each state

Remember that our explorer is an
EpsilonGreedyExplorer(0.1), which will select the turn-left action (the first one of the maximum Q-value) with probability of0.95here
The Training Mode¶
To Optimize the policy, a special policy wrapper is provided in RL.jl: the Agent.
agent = Agent(
policy = policy,
trajectory = VectorSARTTrajectory()
);

The data flow is now changed.
- First, it will be send to the experience replay buffer.
- Then it will be passed to the inner policy to generate the action.
- At proper time, it will extract some random batch of previous experiences and use it to optimize the inner policy
run(agent, env, StopAfterNEpisodes(10), TotalRewardPerEpisode())
Let's take a look into the total length of each episode:
hook = StepsPerEpisode()
run(agent, env, StopAfterNEpisodes(10), hook)
plot(hook.steps[1:end-1])
Q4: Why does it need more than 3 steps to reach our goal?¶
Obviously our best policy only needs 3 steps.
agent
hook = StepsPerEpisode()
run(
QBasedPolicy(
learner=policy.learner,
explorer=GreedyExplorer()
),
env,
StopAfterNEpisodes(10),
hook
)
plot(hook.steps[1:end-1])
Any questions until now?
To apply RL.jl in real world problems:
- How to choose the proper algorithms?
- How to describe the problem in a recognizable way?
Understand the Trajectories¶
]dev ../Trajectories.jl
using Trajectories
t = Trajectories.CircularArraySARTSTraces(;capacity=10)
push!(t; state=4, action=1)
t
push!(t; reward=0., terminal=false, state=3, action=1)
t
push!(t; reward=0., terminal=false, state=2, action=1, )
t
push!(t; reward=-1., terminal=true, state=1, action=1) # this action is meaningness
t
Note that all these behaviors are handled by
Agent
Although the (state, action, reward, terminal) (aks SART here) is the most common one,
each algorithm may have different information to store. You can always create your own ones.
Two Most Commonly Used Algorithms¶
- DQN
- PPO
Thanks to Henri Dehaybe, just wrote how to implement a new algorithm. So I won't cover it here.
env = CartPoleEnv();
plot(env)
ns, na = length(state(env)), length(action_space(env))
rng = StableRNG(123)
policy = Agent(
policy = QBasedPolicy(
learner = BasicDQNLearner(
approximator = NeuralNetworkApproximator(
model = Chain(
Dense(ns, 128, relu; init = glorot_uniform(rng)),
Dense(128, 128, relu; init = glorot_uniform(rng)),
Dense(128, na; init = glorot_uniform(rng)),
) |> cpu,
optimizer = Adam(),
),
batchsize = 32,
min_replay_history = 100,
loss_func = huber_loss,
rng = rng,
),
explorer = EpsilonGreedyExplorer(
kind = :exp,
ϵ_stable = 0.01,
decay_steps = 500,
rng = rng,
),
),
trajectory = CircularArraySARTTrajectory(
capacity = 1000,
state = Vector{Float32} => (ns,),
),
);
stop_condition = StopAfterNSteps(10_000)
hook = TotalRewardPerEpisode()
run(policy, env, stop_condition, hook)
rng = StableRNG(123)
N_ENV = 8
UPDATE_FREQ = 32
env = MultiThreadEnv([
CartPoleEnv(; T = Float32, rng = StableRNG(hash(123 + i))) for i in 1:N_ENV
]);
RLBase.reset!(env, is_force = true)
agent = Agent(
policy = PPOPolicy(
approximator = ActorCritic(
actor = Chain(
Dense(ns, 256, relu; init = glorot_uniform(rng)),
Dense(256, na; init = glorot_uniform(rng)),
),
critic = Chain(
Dense(ns, 256, relu; init = glorot_uniform(rng)),
Dense(256, 1; init = glorot_uniform(rng)),
),
optimizer = Adam(1e-3),
) |> cpu,
γ = 0.99f0,
λ = 0.95f0,
clip_range = 0.1f0,
max_grad_norm = 0.5f0,
n_epochs = 4,
n_microbatches = 4,
actor_loss_weight = 1.0f0,
critic_loss_weight = 0.5f0,
entropy_loss_weight = 0.001f0,
update_freq = UPDATE_FREQ,
),
trajectory = PPOTrajectory(;
capacity = UPDATE_FREQ,
state = Matrix{Float32} => (ns, N_ENV),
action = Vector{Int} => (N_ENV,),
action_log_prob = Vector{Float32} => (N_ENV,),
reward = Vector{Float32} => (N_ENV,),
terminal = Vector{Bool} => (N_ENV,),
),
);
Note the type of policy and Trajectory.
stop_condition = StopAfterNSteps(10_000)
hook = TotalBatchRewardPerEpisode(N_ENV)
run(agent, env, stop_condition, hook)
PPO is one of the most commonly used and also studied algorithms.
The 37 Implementation Details of Proximal Policy Optimization
Since RL.jl is very flexible, most of them are pretty easy/straightforward to implement with RL.jl.
Environments¶
For most simple environments, the interfaces defined in CommonRLInterface.jl would be enough.
reset!(env) # returns nothing
actions(env) # returns the set of all possible actions for the environment
observe(env) # returns an observation
act!(env, a) # steps the environment forward and returns a reward
terminated(env) # returns true or false indicating whether the environment has finishedOr if you prefer the interfaces defiend in RLBase, you can find a lot of examples at RLEnvs.
mutable struct MultiArmBanditsEnv <: AbstractEnv
true_reward::Float64
true_values::Vector{Float64}
rng::AbstractRNG
reward::Float64
is_terminated::Bool
end
function MultiArmBanditsEnv(; true_reward = 0.0, k = 10, rng = Random.GLOBAL_RNG)
true_values = true_reward .+ randn(rng, k)
MultiArmBanditsEnv(true_reward, true_values, rng, 0.0, false)
end
RLBase.action_space(env::MultiArmBanditsEnv) = Base.OneTo(length(env.true_values))
RLBase.state(env::MultiArmBanditsEnv, ::Observation, ::DefaultPlayer) = 1
RLBase.state_space(env::MultiArmBanditsEnv) = Base.OneTo(1)
RLBase.is_terminated(env::MultiArmBanditsEnv) = env.is_terminated
RLBase.reward(env::MultiArmBanditsEnv) = env.reward
RLBase.reset!(env::MultiArmBanditsEnv) = env.is_terminated = falseSeveral important things to consider:
- The state space of the environment
- The size of the state space
- Is there any different representation of the state? (One-hot, multi-hot? Chain consequent states? Split into different layers?)
- The action space of the environment
- Discrete or continuous? (Do you really need continuous action space representation? [binning])
- How large is the action space? Can we reduce the action space futher?
- Legal action masks
- Can we efficiently run multiple replicas together?
What to Expect in the Next Release?¶
- A fresh new implementation of (Async)Trajectories (Enable distributed training)
- Add more experiments on environments with (multi-)continuous action spaces. (Mujoco)
- End2end GPU training (environments running on GPU) (IssacGymEnv)
To be honest, RL.jl is hard to complete with many other mature packages written in Python. Part of the reason is that we lack active contributors & users (kind of a chicken-or-egg problem).
Thank you all!
(Contribution or Cooperation are warmly welcomed!)
HTML(
"""
<style>
@font-face {
font-family: JuliaMono-Regular;
src: url("https://cdn.jsdelivr.net/gh/cormullion/juliamono/webfonts/JuliaMono-Regular.woff2");
}
.rendered_html table{
font-size: 16px !important;
}
div.input_area {
background: #def !important;
font-size: 16px !important;
}
div.output_area pre{
background: #def !important;
font-size: 16px !important;
font-family: JuliaMono-Regular;
}
.CodeMirror {
font-size: 16px !important;
font-family: "JuliaMono-Regular" !important;
font-feature-settings: "zero", "ss01";
font-variant-ligatures: contextual;
}
</style>
"""
)